Consolidation modelling of second grade porous media by homogenization

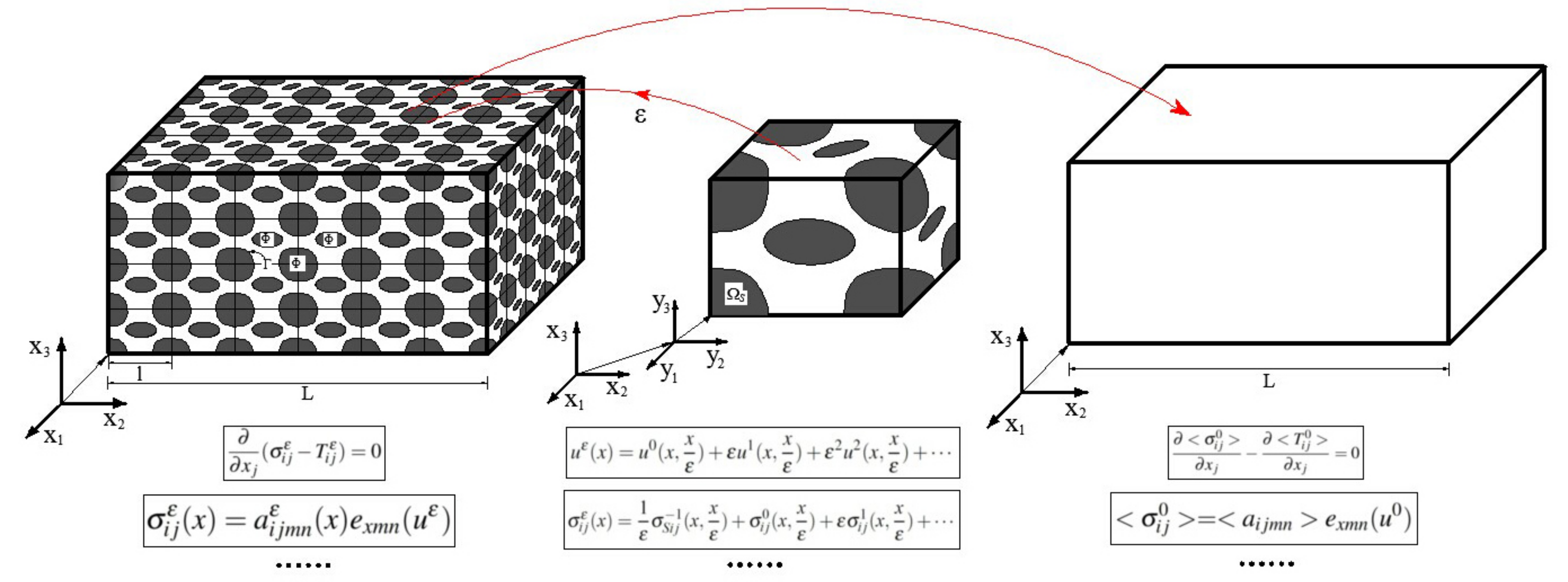
The scope of this mater project is to investigate the macroscopic second grade modeling of a saturated porous matrix by double scale asymptotic expansion method. Strain localization is modeled by the second grade modeling which considered the second derivative displacement, and it is obtained from the virtual power formulation. The homogenization method is used to solve partial differential equations in the heterogeneous materials with a periodic structure. Each quantity (such as displacement, force, stress and water pressure) of the model is expanded (double scale) and was put them into partial differential equations. Then, the mean quantities were obtained a long with the macroscopic second grade models by the homogenization process. The modeling is equivalent to those without any boundary condition of solid or interface condition between solid and fluid inside the sample. In this report we investigated the macroscopic second grade modeling of 1D periodic medium, empty porous matrix and saturated porous matrix.